L espérance de gain à la Roulette Méthode de Hawks
Suite des articles :
- Méthodes gagnantes à la roulette ainsi que l’esperance de gain à laroulette avec la méthode classique
La méthode de Hawks.
Pour aborder l’étude de cette méthode, nous allons qualifier de « série » une suite de plusieurs tours de roulette se terminant par un tirage gagnant. Par exemple, en utilisant les lettres P pour « perdu » et G pour « gagné », une série pourra être constituée de : P, P, P, P, G ou de P, P, G bref, d’une suite de plusieurs pertes terminée par un bon tirage.
La méthode de Hawks peut donc être vue comme une suite de séries plus ou moins longues de ce type avec un gain de 1 euro pour chaque série (voir I.1. la méthode de Hawks).
Les casinos limitant les sommes qui peuvent être jouées en une seule fois, il ne pourra donc être possible de doubler la mise précédente (et donc perdue) qu’un certain nombre de fois. Sur la plupart des casinos en ligne, la mise maximale est souvent 100 fois la mise minimale.
Il ne pourra être possible de doubler que six fois de suite et nous ne pourrons pas supporter 7 pertes consécutives (1, 2, 4, 8, 16, 32, et 64).
Pour notre étude, et afin de pouvoir la généraliser, nous allons poser « n » le nombre de fois consécutifs où il sera possible de jouer avant de tout perdre (dans notre exemple n=7).
Pour n donné (fixé par le casino) et au moment de notre première mise, calculons la probabilité que nous avons de gagner, à savoir de ne pas voir sortir plus de n pertes consécutives.
Pg(n) = probabilité de gagner et Pp(n) = probabilité de perdre.
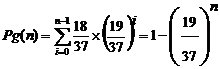 |
et |
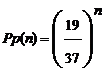 |
La somme que nous risquons de perdre s’obtient en calculant la somme des n premiers termes d’une suite géométrique de premier terme u1 = 1 et de raison q = 2. On obtient alors : – 1.
Nous pouvons donc calculer l’espérance de gain en fonction de n.
E(n) = Pg(n) x 1 – Pp(n) x ( ![]() – 1).
– 1).
En remplaçant Pg(n) et Pp(n) par leurs valeurs respectives et en simplifiant on obtient alors :
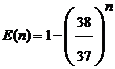 |
Sur la plupart des casinos en ligne Français, vous ne pourrez misez plus de 100 fois la mise minimale sur un tour et donc doubler plus 6 fois consécutives.
Dans ces conditions, pour n=7, votre probabilité de gagner sera de 99% et votre espérance de gain de -0.20 (les résultats sont approximatifs). Cela signifie que vous perdrez en moyenne 20 centimes d’euros pour chaque série, en clair, sur 106 séries, vous gagnerez 105 fois 1 euros et vous perdrez 1 fois 127 euros, soit un bilan total de -22 euros. Rappelons que la méthode classique vous offre une espérance de gain de – 1/37 soit -0.027…
Mais il y a pire… En effet, avez-vous bien observé la formule encadrée donnant E(n) ? Pour commencer, quelque soit la valeur de n, le résultat sera toujours négatif car 38/37>1. Regardez à présent ce qui se passe lorsque n augmente. Plus n sera grand et plus l’espérance deviendra négative, bref :![]()
Cela signifie simplement que plus le casino vous offrira la possibilité de doubler votre mise précédente, plus votre espérance sera à votre désavantage !
On a donc le tord de croire qu’en ayant la possibilité de doubler ad vitam æternam, la méthode deviendra réellement intéressante. Absolument pas ! Car encore une fois, vous oubliez les sommes que vous risquez de perdre. Elles aussi vont accroitre et de manière bien plus spectaculaire que votre probabilité de gagner.
Les casinos n’ont donc aucune raison de limiter cette possibilité de doubler encore et encore. Ils limitent les mises non pas pour contrecarrer les utilisateurs de cette méthode, mais pour se prémunir d’un éventuel « chanceux » qui pourrait faire exploser la banque en gagnant plusieurs fois de suite.
La méthode de hawks améliorée
Nous allons continuer à travailler avec nos séries, à savoir une suite de plusieurs tours de roulettes donnant un résultat défavorable et se terminant par un tirage gagnant. Cette fois-ci, le gain n’est plus de 1 euro pour chaque série, mais de 1 euro pour chaque tour de roulette Française ! (voir I.3. la méthode améliorée).
En ce qui concerne la somme que nous risquons de perdre, elle se trouve en calculant la somme des n premiers termes d’une suite définie par :
![]()
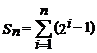
On obtient alors : Somme perdue = ![]()
La probabilité de gagner reste inchangée et dépend du nombre de fois qu’il est possible de doubler la mise perdue
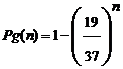 |
et
|
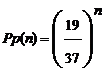 |
La somme que vous gagnerez à la fin de chaque série dépend elle du nombre de fois où vous avez dû doubler votre mise, tout simplement n.
On obtient alors pour le calcul de l’espérance (un peu plus délicate à calculer car il faut cette fois ci considérer tous les cas de figures).
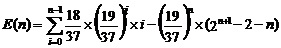
Le résultat se simplifie en utilisant la propriété de la somme des dérivés égale à la dérivée d’une somme (pas de problème de convergence dans cette série). On a alors :
|
|
Pour le cas du casino que nous rencontrerons le plus souvent (mise minimale 1 euro, maximale 100 euros) nous ne pourrons doubler que 5 fois de suite donc n=6. N’oublions pas en effet que nous devons rajouter 1 euro supplémentaire à notre mise après l’avoir doublée : 1, 3, 7, 15, 31 puis 62.
Dans ces conditions E(6) =-0.2925, résultat pire que celui de la méthode de Hawks classique !
En moyenne, sur 53 séries, vous gagnerez 52 fois 2 euros (il est en effet possible de calculer le gain moyen lorsque vous gagnez) et vous perdrez 1 fois 119 euros (1+3+7+15+31+62) soit un bilan de -15 euros.
De plus, si le casino vous offrait la possibilité de doubler bien plus, votre espérance serait encore plus à votre désavantage (là encore la limite de cette espérance est – l’infine).
(p.s. = je tiens à votre disposition tous les détails des calculs précédents).
III) On vous aura prévenu… Un petit bilan pour conclure :
Voilà vos espérances de gain sur une centaine de coups en fonctions de la méthode pratiquée
| Méthode classique |
– 3 euros
|
| Méthode de Hawks |
– 22 euros
|
| Hawks améliorée |
– 30 euros
|
Vous pouvez donc constater que la « meilleure » méthode, ou tout du moins la moins « pire », reste la méthode classique, celle ou vous décidez de placer un jeton où vous voulez sans chercher à faire quoi que ce soit d’autre.
Alors, pourquoi un tel battage sur internet…
Seriez-vous donc aussi naïf ? Allez faire un petit tour sur certains forums (comment ça marche pour ne pas en citer) et allez observer les « internautes » qui louent les bienfaits de ces méthodes… A chaque fois, ils vous conseillent tel ou tel site de casino pour expérimenter leur « trouvaille » miracle et, évidemment, c’est toujours le même.
Ces soi-disant internautes ne sont que de simples publicistes à la solde de ces casinos, rémunérer pour appâter le client.
Ils vous promettent de magnifiques gains alors qu’en réalité (j’espère que vous avez compris maintenant) vous perdrez encore plus vite. L’astuce se trouve dans le fait de vous faire miroiter de belles probabilités de réussite sans vous parler de la question essentielle : l’espérance de gain.
Joueriez-vous à un jeu où vous auriez 99% de chance de gagner 1 million de dollars, à condition d’acheter le billet 100 millions de dollars ? C’est un peu exagéré, mais cela revient à peu près au même.
La meilleure méthode pour jouer à la roulette est donc la suivante :
Le temps, c’est de l’argent. C’est uniquement ce que vous offrent les casinos : du bon temps.
Donc, partez du principe qu’il vous faut utiliser la méthode la plus simple et la plus connue de tous : jouer normalement en vous amusant avec les carrés, les transversales ou les colonnes, et que dans ces conditions vous perdrez en moyenne 3 fois la mise de base tous les 100 coups.
C’est le prix à payer pour s’offrir une bonne tranche d’émotion et de sensations !
Que cela ne reste que du plaisir et pas un moyen de gagner votre vie, vous y laisseriez votre chemise.
Après, vous ne pourrez pas dire qu’on ne vous aura pas prévenu !
*************************************************************************************************************
Merci à Pascal D. pour nous avoir transmis ces calculs sur l’espérance de gain
**************************************************************************************************************
si vous souhaitez tout relire :
Suite des articles :
